Egzamin ósmoklasisty CKE z matematyki 15 maja 2024

Egzamin ósmoklasisty CKE z matematyki z 15 maja 2024 – odpowiedzi (testowa wersja)

Poniżej znajdziesz zadania z egzaminu przeprowadzonego w dniu 15 maja 2024 roku wraz z odpowiedziami oraz pełnymi rozwiązaniami w formie zakładek, które możesz otwierać bądź zamykać (do wersji X, wersja Y ma te same zadania, z inną kolejnością odpowiedzi).
Każde rozwiązanie prezentowane jest w dwóch wersjach: tekstowej z opcją druku, oraz filmu na YouTube.

Natomiast jeśli chciał(a)byś znaleźć z kolei wersję PDF całego arkusza, zapraszam Cię serdecznie na tę stronę:
https://programtica.edu.pl/egzamin-osmoklasisty-matematyka-cke-15-maja-2024/.
Mam nadzieję, że przedstawione poniżej rozwiązania pomogą Ci w nauce! 😊

Treści zadań i rozwiązania

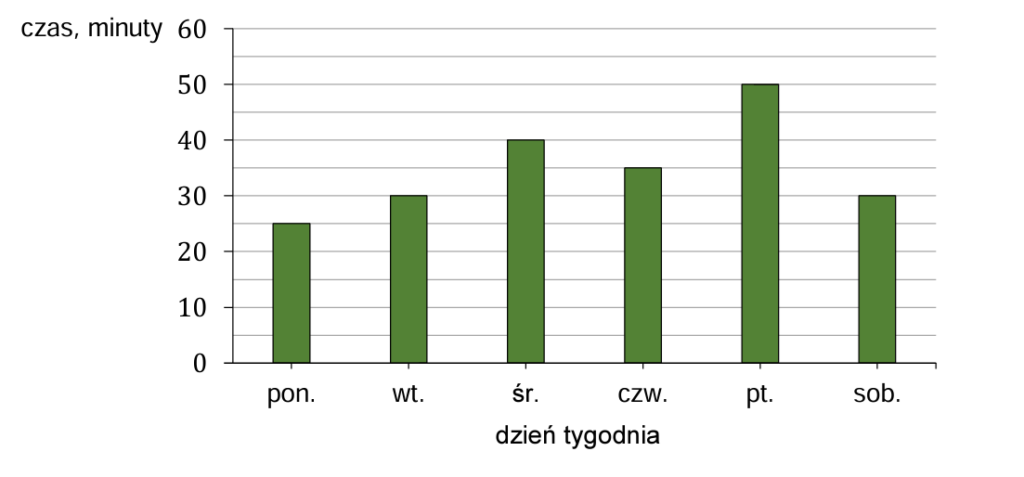
Ala codziennie uczyła się języka hiszpańskiego. Na diagramie przedstawiono, ile czasu przeznaczyła na naukę tego języka w kolejnych dniach tygodnia od poniedziałku do soboty.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Ala przez cztery dni – od poniedziałku do czwartku – na naukę języka hiszpańskiego przeznaczyła łącznie $2$ godziny i $10$ minut.	P	F
Na naukę języka hiszpańskiego w sobotę Ala przeznaczyła o $40\%$ czasu mniej niż w piątek.	P	F

1. Obliczmy, ile łącznie minut Ala spędziła przy nauce języka podczas wspomnianych dni:

$25+30+40+35 = 130 \,\textnormal{min} = 2 \textnormal{ h } 10 \,\textnormal{min}$

Czyli zdanie jest prawdziwe.

2. Sposób I.

Można zastosować proporcję (50 minut odpowiada piątkowi, 30 minut sobocie):

$\begin{array}{ccc} 50 & - & 100\% \\ 30 & - & x\end{array}$

$\begin{array}{cccc} 50\cdot x = 30 \cdot 100\% \\ x = \frac{3\cancel{0} \cdot 100\%}{5\cancel{0}} = \frac{300\%}{5} = 60\%\\\end{array}$

$100\%-60\%=40\%$

Sposób II.

W procentach pojawiał się też temat o nazwie: O ile procent więcej, o ile procent mniej?
Wykonajmy zatem tutaj niezbędne rachunki:

$\frac{50-30}{50}\cdot 100\% = 40\%$

Czyli to zdanie też jest prawdziwe.

W przygotowaniu – po 1 I 2025

Wypisano ułamki spełniające łącznie następujące warunki:

mianownik każdego z nich jest równy $4$
licznik każdego z nich jest liczbą naturalną większą od mianownika
każdy z tych ułamków jest większy od liczby $3$ oraz mniejszy od liczby $5$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich ułamków spełniających powyższe warunki jest

A. sześć.

B. siedem.

C. osiem.

D. dziewięć.

Zwróćmy uwagę, że w treści jest mowa o liczbach $3$ , oraz $5$ . Tych liczb nie będziemy brali pod uwagę przy zliczaniu naszych ułamków (na mocy warunku 3).

Zamieńmy podane powyżej liczby na ułamki niewłaściwe. W tym konkretnym przypadku będą to ułamki o licznikach naturalnych większych niż mianowniki – muszą one wynosić dokładnie $4$ , zgodnie z warunkami 1 i 2:

$\begin{array}{cccc}3=\frac{12}{4}\\\\5=\frac{20}{4}\end{array}$

Wypiszmy zatem wszystkie ułamki podpadające pod nasze warunki. Będą się zatem one mieścić się pomiędzy wskazanymi liczbami z początku:

$\frac{13}{4},\,\frac{14}{4},\,\frac{15}{4},\,\frac{16}{4},\frac{17}{4},\,\frac{18}{4},\,\frac{19}{4}$

Jak zatem widać, ułamków spełniających wszystkie podane powyżej warunki jest dokładnie siedem – odpowiedź B.

W przygotowaniu – po 1 I 2025

Średnia arytmetyczna trzech liczb: $12, 14, k$ , jest równa $16$ .

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Liczba $k$ jest równa $22$ .	P	F
Średnia arytmetyczna liczb: $12, 14, k, 11, 17,$ jest większa od $16$ .	P	F

1. Korzystając z średniej arytmetycznej, otrzymujemy kolejno:

$\begin{array}{c}\frac{12+14+k}{3}=16\\\\26+k=48\\\\k=22\end{array}$

Czyli zdanie jest prawdziwe.

2. Sprawdźmy, co się stanie, jeśli użyjemy obliczone przed momentem $k$ do nowego wyrażenia:

$\begin{array}{c}&\frac{12+14+22+11+17}{5}=\frac{76}{5}=15 \frac{1}{5}<16\end{array}$

To zdanie jest zatem fałszywe.

W przygotowaniu – po 1 I 2025

Dane są dwie liczby $x$ i $y$ zapisane za pomocą wyrażeń arytmetycznych:

$x=\dfrac{4}{5} \cdot \left(-\dfrac{4}{3}\right)$

$y=\dfrac{4}{5} + \left(-\dfrac{4}{3}\right)$

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.

Liczba $y$ jest liczbą $\begin{array}{|c|c|}\hline\textbf{A} & \textbf{B} \\\hline\end{array}$ .

A. ujemną

B. dodatnią

Liczba $x$ jest $\begin{array}{|c|c|}\hline\textbf{C} & \textbf{D} \\\hline\end{array}$ od $y$ .

C. mniejsza

D. większa

1. Obliczmy najpierw wartość $y$ . Pamiętajmy, że mamy tutaj tak naprawdę odejmowanie ułamków, więc najpierw należy doprowadzić obydwa ułamki do wspólnego mianownika:

$y=\frac{4}{5} + \left(-\frac{4}{3}\right)=\frac{12}{15}-\frac{20}{15}=\frac{12-20}{15}=-\frac{8}{15}$

Z tej części widać zatem, że liczba $y$ jest liczbą ujemną – odpowiedź A.

2. Teraz policzmy $x$ . W mnożeniu ułamków licznik mnożymy przez licznik, a mianownik przez mianownik, nie przy tym zapominając o znaku:

$x=\frac{4}{5} \cdot \left(-\frac{4}{3}\right)=-\frac{16}{15}$

Porównajmy teraz liczby $x$ i $y$ ze sobą:

$x=-\frac{16}{15}$

$y=-\frac{8}{15}$

Widać, że $x$ jest liczbą mniejszą od $y$ – zatem jest to odpowiedź C.

W przygotowaniu – po 1 I 2025

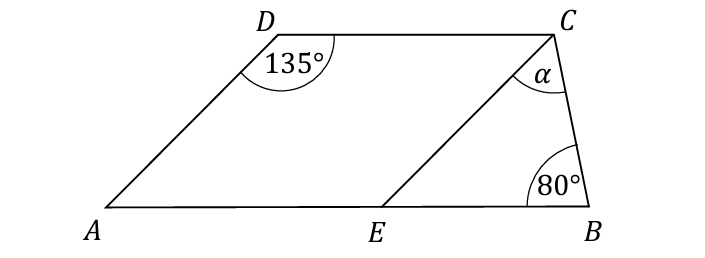
Dany jest trapez $ABCD$ , w którym bok $AB$ jest równoległy do boku $DC$ . W tym trapezie poprowadzono odcinek $EC$ równoległy do boku $AD$ , podano miary dwóch kątów oraz oznaczono kąt $\alpha$ (zobacz rysunek).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Kąt $\alpha$ jest równy:

A. $55^\circ$

B. $50^\circ$

C. $45^\circ$

D. $20^\circ$

Z własności równoległoboku, wiemy że kąty leżące naprzeciw siebie mają taką samą miarę.

Stąd $|\sphericalangle AEC| = |\sphericalangle ADC| = 135^{\circ}$

Zauważmy następnie, że kąt $AEC$ z kątem $CEB$ tworzą dwa kąty przyległe (suma takich dwóch kątów wynosi $180^{\circ}$ ), stąd $|\sphericalangle CEB|=180^{\circ}-135^{\circ}=45^{\circ}$ .

Ponadto wielokąt $EBC$ jest trójkątem – suma miar kątów wewnętrznych w trójkącie wynosi $180^{\circ}$ .

Dlatego też:

$\alpha=|\sphericalangle ECB|=180^{\circ}-(80^{\circ}+45^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$

Co daje już naszą odpowiedź – A.

W przygotowaniu – po 1 I 2025

Dane jest równanie

$5x=\dfrac{y}{w}$ , gdzie $x,y,w$ są różne od $0$ .

Zadaniem Pawła było przekształcanie tego równania tak, aby wyznaczyć $x,y,w$ . Paweł otrzymał trzy równania:

$x=\frac{y}{5w}$

$y=\frac{5x}{w}$

$w=\frac{y}{5x}$

Które z równań I-III są poprawnymi przekształceniami równania $5x=\frac{y}{w}$ ?
Wybierz właściwą odpowiedź spośród podanych.

A. I i II

B. II i III

C. I i III

D. I,II,III

Przekształćmy powyższe równanie ze względu na nasze niewiadome i zobaczmy, do czego dojdziemy.

Zmienna $x$ :

$5x=\frac{y}{w} \Rightarrow x=\frac{y}{5w}$

Zmienna $y$ :

$5x=\frac{y}{w} \Rightarrow y=5xw$

Zmienna $w$ :

$5x=\frac{y}{w} \Rightarrow y=5xw \Rightarrow w=\frac{y}{5x}$

Widać, że jedynie $x$ i $w$ Paweł wyznaczył dobrze, czyli poprawną odpowiedzią jest odpowiedź C.

W przygotowaniu – po 1 I 2025

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Iloczyn $3 \cdot 9^{5}$ jest równy wartości wyrażenia $3^{11}$ .	P	F
Wyrażenie $\frac{2^{8} \cdot \,2^{7}}{2^{10}}$ można zapisać w postaci $2^{5}$ .	P	F

1. Skorzystajmy z dwóch własności potęg działających dla $a>0,m,n \in \mathbb{R}$ :

$\begin{array}{c}(a^{m})^{n}=a^{mn}\\\\a^{m}\cdot a^{n} = a^{m+n}\end{array}$

Zatem:

$3 \cdot 9^{5}=3^{1} \cdot (3^{2})^{5}=3^{1} \cdot 3^{10}=3^{1+10}=3^{11}$

Czyli zdanie jest prawdziwe.

2. Poza drugą własnością z zdania 1., należy skorzystać z jeszcze jednej, dość podobnej własności. Ona też działa dla $a>0,m,n \in \mathbb{R}$ :

$\frac{a^{m}}{a^{n}} = a^{m-n}$

Zatem:

$\frac{2^{8} \cdot \,2^{7}}{2^{10}}=\frac{2^{8+7}}{2^{10}}=\frac{2^{15}}{2^{10}}=2^{15-10}=2^5$

To zdanie też jest prawdziwe.

W przygotowaniu – po 1 I 2025

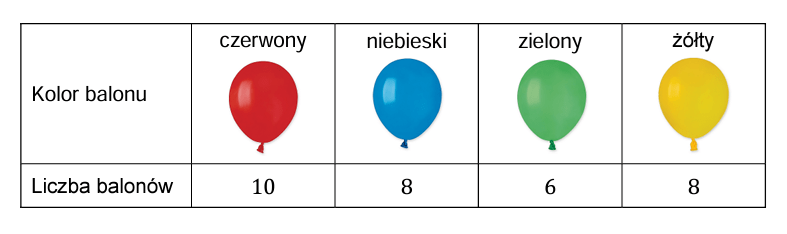
Karolina kupiła jedno pudełko balonów. W tabeli podano informacje dotyczące kolorów balonów oraz ich liczby w tym pudełku.

Karolina wyjmowała losowo po jednym balonie z pudełka. Pierwsze dwa wyjęte balony były w kolorze czerwonym.

Jakie jest prawdopodobieństwo, że trzeci balon losowo wyjęty przez Karolinę będzie w kolorze czerwonym? Wybierz właściwą odpowiedź spośród podanych.

A. $\frac{1}{3}$

B. $\frac{5}{16}$

C. $\frac{4}{15}$

D. $\frac{1}{4}$

Skupmy się na losowaniu w sytuacji, gdy już wylosowaliśmy dwa czerwone balony.

Zostanie tym samym $8$ balonów czerwonych, $8$ balonów niebieskich, $6$ balonów zielonych, $8$ balonów żółtych, czyli wszystkich balonów jest $30$ .

W tej sytuacji prawdopodobieństwo wylosowania jednego czerwonego balona wynosi:

$p=\frac{8}{30}=\frac{4}{15}$

A jest to odpowiedź C.

W przygotowaniu – po 1 I 2025

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wyrażenie $x(x+4)-3(2x-5)$ można przekształcić do postaci

A. $x^2+2x-5$

B. $x^2-2x+5$

C. $x^2+2x-15$

D. $x^2-2x+15$

Przekształćmy podane równanie, włączając wyrażenia do nawiasu, opuszczając nawias ze zmienionym znakiem i redukując wyrazy podobne:

$x(x+4)-3(2x-5)=x^2+4x-(6x-15)=x^2+4x-6x+15=x^2-2x+15$

Jak widać, jest to odpowiedź D.

W przygotowaniu – po 1 I 2025

Podróż pociągiem z Olsztyna do Gdyni planowo trwa $2$ godziny i $54$ minuty. Pewnego dnia pociąg wyjechał z Olsztyna punktualnie o wyznaczonej godzinie, ale przyjechał do Gdyni z czterominutowym opóźnieniem o godzinie $17:31$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pociąg wyjechał z Olsztyna o godzinie

A. $14:27$

B. $14:41$

C. $14:31$

D. $14:33$

Skoro pociąg przyjechał z czterema minutami opóźnienia, to oznacza, że powinien planowo przyjechać o godzinie $17:27$ .

Aby ułatwić obliczenia na czasie, będę działać stopniowo:

$27$ minut wcześniej: $17:00$ .
$2$ godziny wcześniej: $15:00$ .
$27$ minut wcześniej: $14:33$ .

Tym samym doszliśmy do odpowiedzi D.

W przygotowaniu – po 1 I 2025

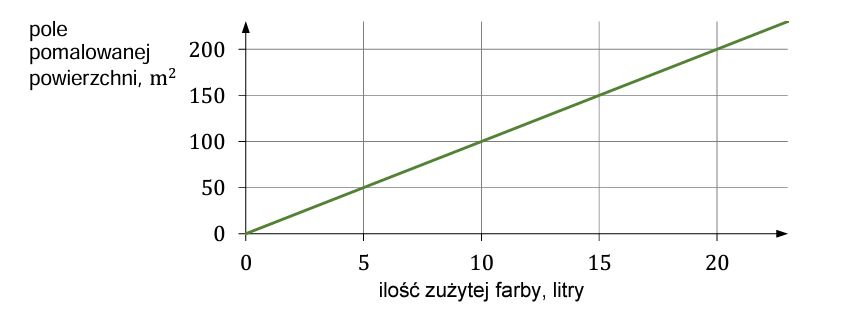
Na wykresie przedstawiono zależność pola pomalowanej powierzchni od ilości zużytej farby. Pole pomalowanej powierzchni jest wprost proporcjonalne do ilości zużytej farby.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

$18$ litrów tej farby wystarczy na pomalowanie $180\,{\text{m}^2}$ powierzchni.	P	F
Na pomalowanie $125\,{\text{m}^2}$ powierzchni wystarczy $12$ litrów tej farby.	P	F

Ponieważ pole pomalowanej powierzchni jest wprost proporcjonalne do ilości zużytej farby, oznacza to, że na każdy litr pomalujemy dokładnie tyle samo powierzchni. Na potrzeby tego zadania przyjmujemy sytuację idealną – tzn. malujemy zawsze równomiernie – w praktyce niestety tak nie będzie, więc zawsze warto dokupić więcej farby.

Obliczmy zatem, ile powierzchni pomalujemy na każdy litr farby:

$\frac{50\,{\text{m}^2}}{5}=10\,{\text{m}^2}$

1. Malując $18$ litrów, otrzymamy tym samym:

$18\cdot 10\,{\text{m}^2} = 180\,{\text{m}^2}$

To zdanie jest zatem prawdziwe.

2. Gdybyśmy użyli $12\,{l}$ , to byśmy pomalowali:

$12\cdot 10\,{\text{m}^2} = 120\,{\text{m}^2}$

Czy to wystarczy, aby pomalować pożądaną przez nas powierzchnię? Oczywiście nie! Musielibyśmy użyć $12{,}5\,{l}$ farby, aby pomalować $125\,{\text{m}^2}$ powierzchni.

Zdanie to jest zatem zdaniem fałszywym.

W przygotowaniu – po 1 I 2025

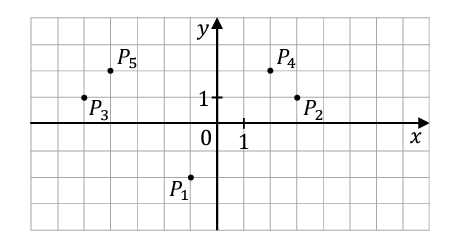
Podróż pociągiem z Olsztyna do Gdyni planowo trwa $2$ godziny. W układzie współrzędnych $(x,y)$ zaznaczono pięć punktów $P_{1}, P_{2}, P_{3}, P_{4}$ oraz $P_{5}$ (zobacz rysunek). Wszystkie współrzędne tych punktów są liczbami całkowitymi. Punkt $P_{1}$ ma współrzędne $(-1,-2)$ .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Jeżeli współrzędną $x$ punktu $P_{1}$ zwiększymy o $4$ , a współrzędną $y$ tego punktu zwiększymy o $3$ , to otrzymamy współrzędne punktu

A. $P_{2}$

B. $P_{3}$

C. $P_{4}$

D. $P_{5}$

Uwzględnijmy podane współrzędne punktu $P_{1}$ i wykonajmy na nich rachunki. Oznaczmy współrzędne nowego punktu przez $(x_{1},y_{1})$ :

$x_{1} = (-1)+4 = 3$
$y_{1} = (-2)+3 = 1$

Punktem o współrzędnych $(x_{1}, y_{1})=(3,1)$ jest punkt $P_{2}$ .

A zatem jest to odpowiedź A.

W przygotowaniu – po 1 I 2025

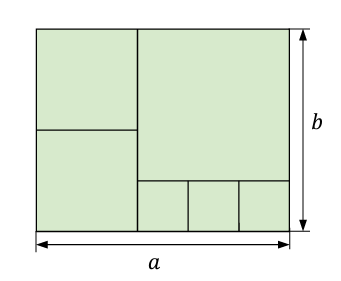
Na rysunku przedstawiono prostokąt o bokach długości $a$ i $b$ podzielony na sześć kwadratów.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Stosunek długości boków $a:b$ tego prostokąta jest równy

A. $6:5$

B. $5:4$

C. $4:3$

D. $3:2$

Przeanalizujmy poniższy rysunek:

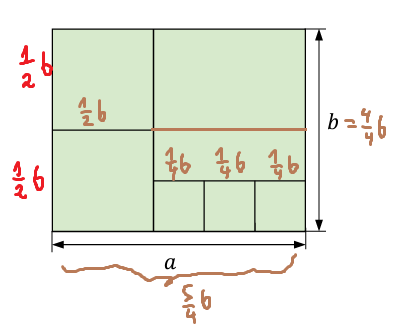
Na podstawie rysunku można przekonać się, że odcinek $b$ jest zbudowany z kilku mniejszych odcinków. Mają one długość: $\frac{1}{2}b,\frac{1}{4}b, \frac{1}{4}b$ . To prowadzi nas do obserwacji, że odcinek $a$ musi składać się z odcinków długości $\frac{1}{2}b,\frac{1}{4}b, \frac{1}{4}b,\frac{1}{4}b$ – czyli $\frac{5}{4}b$ .

A zatem stosunek boków wynosi:

$\frac{a}{b}=\frac{\frac{5}{4}b}{\frac{4}{4}b}=\frac{5}{4}$

Jest to odpowiedź B.

W przygotowaniu – po 1 I 2025

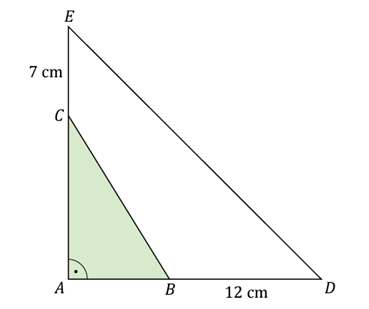
W trójkącie prostokątnym $ABC$ przyprostokątną $AC$ wydłużono o $7\,{\text{cm}}$ , a przyprostokątną $AB$ wydłużono o $12\,{\text{cm}}$ i otrzymano trójkąt prostokątny równoramienny $ADE$ o polu równym $200 \,{\text{cm}^2}$ (zobacz rysunek).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Przyprostokątna trójkąta $ADE$ jest równa $20\,{\text{cm}}$ .	P	F
Pole trójkąta $ABC$ jest równe $52 \,{\text{cm}^2}$ .	P	F

Warto to zadanie rozpocząć od przeanalizowania dokładnie naszych zdań.

1. Obliczymy długość przyprostokątnej trójkąta, korzystając ze wzoru na pole trójkąta (w tym przypadku podstawa, jak i wysokość trójkąta mają taką samą długość $a$ , na podstawie informacji z treści zadania – trójkąt jest prostokątny równoramienny):

$\begin{array}{c}200 \,{\text{cm}^2}=\frac{a \cdot a}{2}\\[0.05cm]400 \, cm^{2}=a^{2}\\a=20\,{\text{cm}}\hspace{0.5cm} \textnormal{lub}\hspace{0.5cm} a=-20\,{\text{cm}}\end{array}$

Oczywiście długość przyprostokątnej nie może być ujemna, zatem przyprostokątna będzie mieć długość $a=20\,{\text{cm}}$ .

W takim razie zdanie będzie prawdziwe.

2. Obliczmy długość boków $AB$ i $AC$ :

$|AB|=20\,{\text{cm}}-12\,{\text{cm}} = 8\,{\text{cm}}$
$|AC|=20\,{\text{cm}}-7\,{\text{cm}} = 13\,{\text{cm}}$

Dlatego też:

$P_{ABC}=\frac{|AB| \cdot |AC|}{2}=\frac{8\,{\text{cm}} \, \cdot \, 13\,{\text{cm}}}{2} = \frac{104\,\text{cm}^{2}}{2} = 52\,{\text{cm}^2}$

To zdanie jest prawdziwe.

W przygotowaniu – po 1 I 2025

Dany jest ostrosłup prawidłowy czworokątny. Pole powierzchni całkowitej tej bryły jest równe $P$ , a jedna ściana boczna ma pole równe $\frac{2}{9}P$ .

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.

Pole powierzchni bocznej tego ostrosłupa jest równe $\begin{array}{|c|c|}\hline\textbf{A} & \textbf{B} \\\hline\end{array}$ .

A. $\frac{6}{9}P$

B. $\frac{8}{9}P$

Pole powierzchni podstawy tego ostrosłupa jest dwa razy $\begin{array}{|c|c|}\hline\textbf{C} & \textbf{D} \\\hline\end{array}$ niż pole powierzchni jego jednej ściany bocznej.

C. mniejsze

D. większe

Naszkicujmy rysunek poglądowy do zadania:

Widać, że mamy 4 ściany boczne – każda ze ścian bocznych ma pole $\frac{2}{9}P$ . Tym samym:

$P_{b}=4\cdot\frac{2}{9}P=\frac{8}{9}P$

Taki wynik mamy w odpowiedzi B.

Dzięki temu obliczymy pole podstawy. Jest ono równe:

$P_{p}=P_{c}-P_{b}=P-\frac{8}{9}P=\frac{1}{9}P$

Zatem pole podstawy jest dwa razy mniejsze od pola jednej ściany bocznej – odpowiedź C.

W przygotowaniu – po 1 I 2025

Ela i Ania dostały w prezencie po jednym zestawie puzzli o takiej samej liczbie elementów. Ela ułożyła $\frac{2}{5}$ swoich puzzli, a Ania $\frac{1}{3}$ swoich. Dziewczynki ułożyły łącznie $440$ elementów.

Oblicz, z ilu elementów składa się jeden zestaw puzzli. Zapisz obliczenia.

Jeden zestaw puzzli składa się z $600$ elementów.

Zadanie to polega na rozwiązaniu równania z jedną niewiadomą.

Niech $x$ oznacza całkowitą liczbę elementów puzzli.

Wtedy:

$\begin{array}{c}\frac{2}{5}x+\frac{1}{3}x=440\\[0.2cm]\frac{6}{15}x+\frac{5}{15}x=440\\[0.2cm]\frac{11}{15}x=440\hspace{0.25cm}/ \cdot 15\\[0.2cm]11x=6600\\[0.2cm]x=600\end{array}$

W przygotowaniu – po 1 I 2025

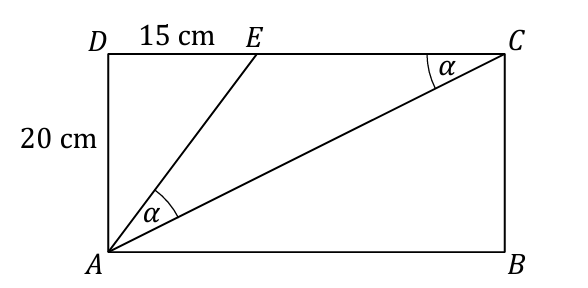
Prostokąt $ABCD$ podzielono na trzy trójkąty: $AED, ACE, ABC$ (zobacz rysunek). Na rysunku podano również długości dwóch boków trójkąta $AED$ oraz zaznaczono dwa kąty trójkąta $ACE$ , o takiej samej mierze $\large{\alpha}$ .

Oblicz pole trapezu $\mathbf{\mathit{ABCE}}$ . Zapisz obliczenia.

Pole trapezu $\mathbf{\mathit{ABCE}}$ jest równe $650\,{cm^2}$ .

Przypomnijmy wzór na pole trapezu:

$P=\frac{(a+b)\,\cdot\,h}{2}$

We wzorze tym $a,b$ są podstawami trapezu, natomiast $h$ to wysokość.

Póki co jedynie znamy długość odcinka $BC$ , który jest jednocześnie wysokością – $h$ . Wynosi ona $20\,{\text{cm}}$ , tak jak wysokość trójkąta prostokątnego $ADE$ .

Zastanówmy się, co teraz moglibyśmy policzyć. Okazuje się, że w trójkącie prostokątnym o którym była mowa powyżej, możemy obliczyć przeciwprostokątną, z twierdzenia Pitagorasa:

$\begin{array}{c}20^2+15^2=c^2\\[0.3cm]400+225=c^2\\[0.3cm]625=c^2\hspace{0.25cm}/\,\sqrt{}, c>0\\[0.3cm]c=25\,{\text{cm}}\end{array}$

Zauważmy teraz, że trójkąt $ACE$ jest trójkątem równoramiennym, w którym bok $CE$ ma taką samą długość, jak policzona przed momentem przeciwprostokątna.

Daje to nam zatem długość górnej podstawy – $25\,{\text{cm}}$ , ale również dolnej – jej długość to $15+25=40\,{\text{cm}}$ , a to z tego powodu, że dolna podstawa składa się z odcinków o takiej samej długości, jak boki $DE$ i $EC$ .

W takim razie jesteśmy gotowi do podstawienia wszystkich danych do gotowego wzoru:

$P=\frac{(a+b)\,\cdot\,h}{2} = \frac{(25\,{\text{cm}}+40\,{\text{cm}})\,\cdot\,20\,{\text{cm}}}{2}=\frac{65\,{\text{cm}}\,\cdot\,20\,{\text{cm}}}{2}=65\,{\text{cm}}\,\cdot10\,{\text{cm}}=650\,{\text{cm}}^2$

W przygotowaniu – po 1 I 2025

Pan Jan sprzedał w swoim sklepie $120\, \textnormal{kg}$ truskawek. Połowę masy tych truskawek sprzedał w dużych opakowaniach, $10\%$ masy truskawek – w średnich, a pozostałe truskawki w małych opakowaniach. W tabeli podano informacje dotyczące sprzedaży truskawek w sklepie pana Jana.

SKLEP U JANA
Rodzaj opakowania	Masa truskawek w opakowaniu	Cena opakowania z truskawkami
duże	$1\,\textnormal{kg}$	$18\,\textnormal{zł}$
średnie	$0{,}5\,\textnormal{kg}$	$10\,\textnormal{zł}$
małe	$0{,}25\,\textnormal{kg}$	$6\,\textnormal{zł}$

Oblicz, jaką kwotę otrzymał pan Jan ze sprzedaży wszystkich truskawek. Zapisz obliczenia.

Pan Jan otrzymał ze sprzedaży wszystkich truskawek $2472\, \textnormal{zł}$ .

Obliczmy najpierw poszczególne masy truskawek.

Duże:

$\frac{1}{2} \cdot 120\,\textnormal{kg} = 60\,\textnormal{kg}$

Średnie:

$10\% \cdot 120\,\textnormal{kg} = \frac{10}{100} \cdot 120\,\textnormal{kg} = \frac{1}{10} \cdot 120\,\textnormal{kg} = \frac{120\,\textnormal{kg}}{10}=12\,\textnormal{kg}$

Małe:

$120\,\textnormal{kg}-60\,\textnormal{kg}-12\,\textnormal{kg}=120\,\textnormal{kg}-72\,\textnormal{kg}=48\,\textnormal{kg}$

Kolejnym krokiem jest uwzględnienie masy opakowania, oraz ceny odpowiadającym poszczególnym porcjom truskawek. Aby ułatwić obliczenia, zaprezentuję je w poniższej tabeli:

Porcje truskawek	Łączna waga truskawek	Łączna liczba opakowań	Łączna cena
Duże	$60\,\textnormal{kg}$	$60:1=60$	$60\cdot\,18\,\textnormal{zł}=1080\,\textnormal{zł}$
Średnie	$12\,\textnormal{kg}$	$12:0{,}5=24$	$24\cdot\,10\,\textnormal{zł}=240\,\textnormal{zł}$
Małe	$48\,\textnormal{kg}$	$48:0{,}25=192$	$192\cdot\,6\,\textnormal{zł}=1152\,\textnormal{zł}$

Ostatecznie mamy zatem:

$1080\,\textnormal{zł}+240\,\textnormal{zł}+1152\,\textnormal{zł}=2472\,\textnormal{zł}$

W przygotowaniu – po 1 I 2025

Z trzech jednakowych klocków w kształcie sześcianu i jednego klocka w kształcie ostrosłupa prawidłowego czworokątnego zbudowano dwie wieże (zobacz rysunek). Krawędź sześcianu ma długość $10\,\text{cm}$ . Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość $9\,\text{cm}$ , a jego objętość jest równa $324\,\text{cm}^{3}$ .

Oblicz różnicę wysokości obu wież. Zapisz obliczenia.

Różnica wysokości obu wież wynosi $2\,\text{cm}$ .

Zauważmy, że wysokość pierwszej wieży to wysokość sześcianu oraz ostrosłupa, natomiast drugiej to dwie wysokości sześcianu.

Przypomnijmy, że w sześcianie wszystkie krawędzie mają taką samą długość, wobec czego wysokość pokrywa się co do długości z krawędzią podstawy.

Zatem wysokość II wieży wynosi:

$10\,\text{cm}+10\,\text{cm}=20\,\text{cm}$

W przypadku I wieży musimy wpierw policzyć wysokość, ze wzoru na objętość ostrosłupa. Odnotujmy tylko, że ostrosłup ten ma w podstawie kwadrat.

$\begin{array}{c}V=\frac{1}{3}PpH\\[0.1cm]324 = \frac{1}{3}\cdot 9^2 \cdot H\\[0.1cm]324 = \frac{1}{3}\cdot81\cdot H\\[0.1cm]324 = 27H\\[0.1cm]H=12\,\textnormal{cm}\end{array}$

Wobec tego, wysokość I wieży wynosi:

$10\,\textnormal{cm}+12\,\textnormal{cm}=22\,\textnormal{cm}$

Zatem różnica wysokości obu wież to:

$22\,\textnormal{cm}-20\,\textnormal{cm}=2\,\textnormal{cm}$

W przygotowaniu – po 1 I 2025

Ostatnia aktualizacja: 21 XII 2024, 23:02

W przygotowaniu

Zadania

Powrót do strony z arkuszem

Widzisz gdzieś błąd w rozwiązaniu jakiegoś zadania? Nie rozumiesz jakiegoś fragmentu?
A może znasz inny sposób na jego rozwiązanie i chciał(a)byś się nim pochwalić?
Podziel się wiadomością z nami, chętnie skorzystamy z Twoich uwag!

Subskrybuj

0 komentarzy

najstarszy

najnowszy oceniany

Inline Feedbacks

View all comments