Wyobraź sobie że siadasz przy biurku, które do Ciebie przyjechało całkiem niedawno. Przed Tobą pojawiło się bowiem niespodziewanie nowe zadanie, zupełnie dotychczas nieznane. Masz je wykonać, ale utrudnieniem jest fakt, że nie możesz otrzymać żadnych wskazówek od drugiej osoby dopóki z nim nie powalczysz. Spodziewam się, że Twoja reakcja na jego realizację może być naprawdę różna, w zależności, czy dany problem będziesz w stanie rozwiązać, czy nie. Tak będzie na każdym etapie wykonywania powierzonej pracy, oraz w warunkach, w których obecnie się znajdziesz. Możesz być szczęśliwy gdy poradzisz sobie z wyzwaniem, albo wręcz przeciwnie – sfrustrowany, gdy Ci ono nie wyjdzie 😔
Pisząc ten artykuł zastanawiałem się co może być przyczyną, że matematyka uchodzi w polskich warunkach za przedmiot dość trudny, nieprzystępny. Uznałem więc, że przedstawię poniżej kilka rad, które możesz wdrożyć praktycznie wszędzie – czy to jesteś w domu, czy w szkole. Dzięki temu będziesz mógł jeszcze lepiej uczyć się matematyki, a może i odniesiesz pierwsze sukcesy. Możesz kliknąć w poniższy spis treści, aby przejść do danej wskazówki 😉
Spis treści
- Dobrze się przygotuj przed przystąpieniem do pracy
- Czytaj polecenia starannie i w razie potrzeby wiele razy
- Starannie zapisuj kroki swoich działań i rozwiązań
- Sprawdzaj jak rozwiązałaś(eś) dane rozwiązanie
- Ucz się na popełnionych błędach
- Korzystaj z dostępnych źródeł
- Rozwiązuj zadania samodzielnie
- Próbuj ułożyć podobne zadania
Mamy nakreślony plan działania, to zaczynamy! Gotowi?
Rys. 1. Odpoczywająca żaba. Obraz cyfrowy (na licencji Public Domain), https://pxhere.com/pl/photo/839390
Pierwszą i to bardzo ważną rzeczą jeśli chodzi o naukę matematyki – jest… zmiana podejścia do podejmowanego wyzwania 😉
Aby móc naprawdę efektywnie rozwiązywać zadania matematyczne, obowiązkowo powinieneś być wyspany, wypoczęty, oraz najedzony (z naciskiem na zdrowe jedzenie). Możesz przed rozpoczęciem rozwiązywania zadań wykonać ulubione ćwiczenie (np. artystyczne lub sportowe). Niektórzy uważają, że warto też rozwiązywać sudoku, krzyżówki, oraz zagadki matematyczne. Więcej na ten temat porozmawiamy jeszcze w artykule: ,,5 wskazówek jak dobrze pracować” (w momencie premiery bieżącego artykułu, artykuł ten jest w fazie wczesnych przygotowań).
Z drugiej strony nie jest dobrze jeśli przystępujesz do pracy zestresowany, nie śpisz za długo, grasz bardzo długo w gry komputerowe. Łatwo wówczas o chociażby utratę koncentracji, Twoja reakcja może się zdecydowanie spowolnić…
Druga sprawa – to sposób, w jaki należy czytać polecenia do powierzonego Tobie zadania.
Ktoś może powiedzieć: ,,A co tam, przeczytam zadanie raz, w sumie to mi wisi, czy zrozumiem o co tam chodzi…”
Co o takim postępowaniu sądzisz, gdy masz przed sobą duży sprawdzian, egzamin? Też tak zrobisz?
W takim postępowaniu jest co najmniej kilka pułapek:
- zadania na które natrafisz mogą być bardzo różnego typu (np. z treścią, prawda-fałsz, dobieranie, zadanie dowodowe, etc.),
- niektóre z zadań rozwiązuje się nie posiadając wcześniej wszystkich informacji ,,od ręki” – zrealizowanie danego etapu może wymagać pomyślenia, obrania strategii bazując na tym co zostało podane,
- traktując powierzchownie podaną informację może okazać się, że nie będziesz w stanie rozwiązać danego problemu,
- nie czytając uważnie polecenia, możesz bardzo łatwo skupić swoją uwagę na rzeczach, które są niepotrzebne jeżeli chodzi o rozwiązanie zadania,
- wreszcie… w dobie egzaminów, w przypadku czytania ,,na opak” danej rzeczy, możesz stracić… punkty, które by były Tobie potrzebne do rekrutacji ☹
Rys. 2. Kot czytający książkę. Opracowanie własne na podstawie AI dostępnego na stronie https://pixlr.com/pl/image-generator/
Morał z tego płynie taki że warto czytać ze zrozumieniem zadania, przynajmniej kilka razy. Powiem więcej – jeśli zadanie jest zbyt skomplikowane, warto podzielić je na etapy. Nawet nie wiesz, jak wielu uczniów chce zrobić zadania na raz, ,,jednym tchem”. Z obowiązku redakcyjnego dodam, że Sir Andrew Wiles (1953-) brytyjski matematyk, zamieścił dowód Wielkiego Twierdzenia Fermata na ponad 100 stronach. Także na pewno na raz tego problemu nie zrobił 😉
Twierdzenie to głosi:
Tak na marginesie, pamiętasz jak nazywa się twierdzenie wykorzystujące przypadek n=2? Podpowiem, że jest to jedno z najważniejszych twierdzeń w matematyce – związane z trójkątami 😉
Abstrahując od twierdzenia, nadal nie czujesz się przekonany odnośnie uważnego czytania, ze zrozumieniem? Przeczytaj, co inni powiedzieli na ten temat 😉 Jak się okazuje, taka umiejętność przydaje się także na innych przedmiotach:
Co do czytania uważnie poleceń, biologia rozszerzona nauczyła mnie precyzji w języku i czepiania się literówek – np. amyloza i amylaza znaczą coś innego.
(Katarzyna Kroker, 6 II 2024)
Jeśli chodzi o poziom szkoły ponadpodstawowej, można nie wykonać wszystkich poleceń, np. przy zadaniach optymalizacyjnych uczeń znajdzie poszukiwane długości krawędzi prostopadłościanu, a nie doda informacji o jego objętości, którą to należało według polecenia obliczyć. Natomiast w sytuacji szkoły podstawowej – niech za przykładem będzie zadanie: Objętość prostopadłościanu o danych krawędziach podanych w różnych jednostkach i podaj ją w litrach, a uczeń obliczy i zostawi ją np. w cm^3.
(Kinga Piąstka, 7 II 2024)
Warto czytać ze zrozumieniem, ponieważ sporą część egzaminu możesz poświęcić na zadanie, które będziesz rozwiązywał błędnie. Dlatego lepiej podkreślać sobie te ważne elementy polecenia i wypisywać sobie wszystkie dane.
(Joanna Grendysa, 7 II 2024)
No właśnie… W wypowiedzi Pani Asi kryje się coś bardzo ważnego – zarówno wypisanie wszystkich danych, jak i ich podkreślenia.
Rzeczywiście, to pomaga. Ma to miejsce szczególnie w zadaniach tekstowych, czy tych, które wykorzystują wyrażenia algebraiczne. Ponieważ nie samymi zadaniami tekstowymi matematyk szkolny żyje, ja pójdę o kilka kroków dalej, a mianowicie:
- Numeruj zadania, które robisz (podając numer zadania, oraz jego strony, o ile jest taka możliwość, czasem też źródło z jakiego materiału pochodzi).
- Przepisz całe działanie, dopiero na samym końcu wpisz jego wynik.
- Będzie dobrze, jeśli zapiszesz odpowiedź po rozwiązaniu zadania.
- Tam gdzie trzeba zrobić rysunek, staraj się go robić możliwie jak najdokładniej, warto zrobić też go dość dużego. Pamiętaj jednak, że ma być to tylko rysunek poglądowy (pomocniczy) 😉
Dodam również, że zapisanie chociażby najprostszych działań, potrzebnych do zadania, może wydatnie pomóc w jego rozwiązaniu.
Prześledźmy teraz przykłady rozwiązań kilku zadań. Co o nich możesz powiedzieć? Czy są poprawne? Jeśli nie, co można by zrobić, aby były poprawne? No i wreszcie – czy da się ustalić ich poprawność?
Rys 3,4,5. Przykładowe zadania. Źródło: opracowanie własne, na bazie podręcznika Nowej Ery.
Czasem może się zdarzyć, że w którymś momencie rozwiązywania zadań popełnisz błąd. Oczywiście, niekiedy ten błąd może być mniejszy, lub większy – może też dotknąć w różnej sytuacji. Co warto zrobić w takich sytuacjach?
Rys 6. Zadanie na kolejność wykonywania działań z błędami oraz właściwym rozwiązaniem. Źródło: opracowanie własne, na bazie podręcznika Nowej Ery.
Zadania matematyczne też tutaj przychodzą Ci z pomocą – sprawdzaj swoje rozwiązania. Praktyka pokazuje, że w przypadku złej odpowiedzi najlepiej ją przekreślić – chociaż zauważam, że uczniowie zazwyczaj zmazują błędne obliczenia (to chyba pozostałość po robieniu wielu rzeczy ołówkiem lub co gorsza… zmazywalnym długopisem).
Niekiedy swój błąd można odkryć, wykonując… działanie odwrotne do akurat rozpatrywanego 😉 Tak jest np. w odejmowaniu i dzieleniu, bardzo często sprawdza się je odpowiednio dodawaniem i mnożeniem.
Warto sobie na samym początku uświadomić jedną bardzo ważną rzecz – nie ma ludzi którzy są w 100% bezbłędni 😉 Przypomnę też, że reakcje na dane zdarzenie mogą być całkowicie odmienne.
Zastanów się teraz, czyja reakcja na popełniony błąd jest Tobie najbliższa, oraz odpowiedz sobie na pytanie: Czy taka reakcja jest słuszna?
Tosia: Nie ma na to pytanie odpowiedzi w podręczniku, internecie… Nie umiem tego zrobić, rzucam to!
Zuzia: Mam to zrobione! Hurra! Sprawdzenia nie zrobię, bo po co? Teraz idę pograć w koszykówkę i nie przeszkodzicie mi w tym nic a nic 😉
Karolina: Tu na pewno jest błąd w odpowiedziach z podręcznika – jestem tego całkowicie pewna! Bo niby co tutaj zrobiłam źle?
Grzesiek: Walczę z tym zadaniem już dwie godziny… a i tak to na nic – jestem do niczego, jestem tak tragicznym uczniem…
Hieronim: A no tak… Nie wyszło mi to zadanie… Za bardzo tutaj się pospieszyłem – trzeba było trochę wolniej i uważniej je przeczytać. Przyłożę się bardziej i spróbuję jeszcze raz je rozwiązać!
Pewnie zauważyłaś(eś), że na lekcji matematyki obok przyborów do pisania i rysowania, masz do dyspozycji zeszyty, podręcznik, nierzadko też zbiór zadań.
Zapytasz się – a po co mi to wszystko? Przecież na sprawdzianie, egzaminie mieć tego nie można…
Wtedy powiem Tobie: A chciał(a)byś się nauczyć tego przedmiotu, chcesz mieć lepsze oceny, zdać egzamin na najwyższy wynik? Warto wykorzystać zeszyt, podręcznik w codziennej pracy, zrobieniu zadań domowych, o ile takowe są – często do zadań dołączone są odpowiedzi, tak abyście mogli się… sprawdzić 😊
Na koniec tego punktu, dwie małe uwagi:
Wszystko to dlatego, ponieważ są to tematy na osobne artykuły 😉
Dochodzimy do kolejnej, bardzo ważnej kwestii. Jak myślisz, w jaki sposób najlepiej wykonywać powierzone zadania?
Co do zasady, zadania starajmy się rozwiązywać samodzielnie. Co też bardzo ważne – nie ma sensu najmniejszego ściągać rozwiązania od koleżanki czy kolegi, albo spisywać z Internetu.
Po pierwsze – kiedyś może to wyjść na jaw, jak nie przez kolegów, to przez nauczyciela, egzaminatora.
Po drugie – nie uczysz się wtedy odpowiedzialności za zrobioną pracę – w przypadku kolejnych tematów możesz mieć kłopoty ze zrozumieniem materiału 😔
No i wreszcie po trzecie – jaka byłaby satysfakcja z rozwiązanego przez Ciebie problemu, jeśli tak naprawdę rozwiązanie zostało wykonane po linii najmniejszego oporu?
Samodzielne rozwiązanie problemu jest kluczowe w nauce matematyki.
Rys 7. Pani i Pan analizujący zadania. Obraz cyfrowy (na licencji Public Domain), https://pxhere.com/pl/photo/1085374
Owszem, można sprawdzić rozwiązanie zadania, gdy skończyło się je rozwiązywać, korzystając z odpowiedzi z podręcznika. Jednak nie może być tak, że cała robota ma być wykonana za Ciebie, bez podjęcia choćby najmniejszego wysiłku z Twojej strony.
Dotychczas mówiliśmy o tym, w jaki sposób podchodzić do nauki, jak brać się za rozwiązania zadań. Nie jest już też dla nas problemem, jak reagować na napotkany błąd, w jaki sposób sprawdzać swoje odpowiedzi i rezultaty.
Załóżmy jednak, że wiedza, którą pragniemy posiąść po rozwiązaniu tych zadań, jest dla nas niewystarczająca, ponieważ czujemy, że zbyt słabo jeszcze rozumiemy dany temat. Co wtedy zrobić?
Na pewno wiesz, że sportowcy aby osiągnąć sukces, potrzebują regularnego, solidnego treningu. Nie inaczej jest z nami – jeśli chcemy być dobrymi matematykami, musimy nieustannie ćwiczyć. Można to zrealizować, np. układając zadania pomocnicze, ewentualnie ,,przedłużać” już istniejące – albo też próbując podejść do zrobienia zadania w inny sposób.
Podam poniżej przykład takiego zadania z matury podstawowej CKE z roku 2023, w formule 2015:
32. Wykaż, że dla każdej liczby rzeczywistej x \neq 1 i dla każdej liczby rzeczywistej y prawdziwa jest nierówność
x^2+y^2+5>2x+4y
Nie jest to jedyna droga na rozwiązanie tego zadania. To zadanie można zrobić na minimum… sześć sposobów 😯
Epilog
Dotarliśmy płynnie do końca artykułu. Mam nadzieję, że udało mi się chociaż troszkę zmienić Twoje podejście do nauki matematyki, jeśli dotychczas próby spełzły na niczym.
Niezależnie od sytuacji, w jakiej się znajdujesz – życzę Ci powodzenia w przyszłości i do zobaczenia na moim kanale!
W materiale Autor korzystał ze źródeł, takich jak:
- Braun, M., Mańkowska, A., Paszyńska, M. (2021). Matematyka z kluczem. Podręcznik do matematyki dla klasy czwartej szkoły podstawowej, Część 1, str. 8-12.
- Pólya, G. (1964). Jak to rozwiązać, tłum. L. Kubik, Wydawnictwo Naukowe PWN, Warszawa.
- Wiles, A. (1995). Modular elliptic curves and Fermat’s Last Theorem. Annals of Mathematics. 141 (3): 443–551.
- CKE. Strona główna Centralnej Komisji Egzaminacyjnej. online; dostęp 13 lutego 2024, url: https://www.cke.gov.pl.
- obserwacje własne
Gorące podziękowania dla Pań Katarzyny, Kingi, oraz Joanny – za podzielenie się zdaniem na temat czytania ze zrozumieniem, oraz wyrażeniem zgody na publikację ich przemyśleń.
Imiona postaci pojawiających się w punkcie 5. zostały wymyślone i nie są powiązane z konkretnymi osobami.




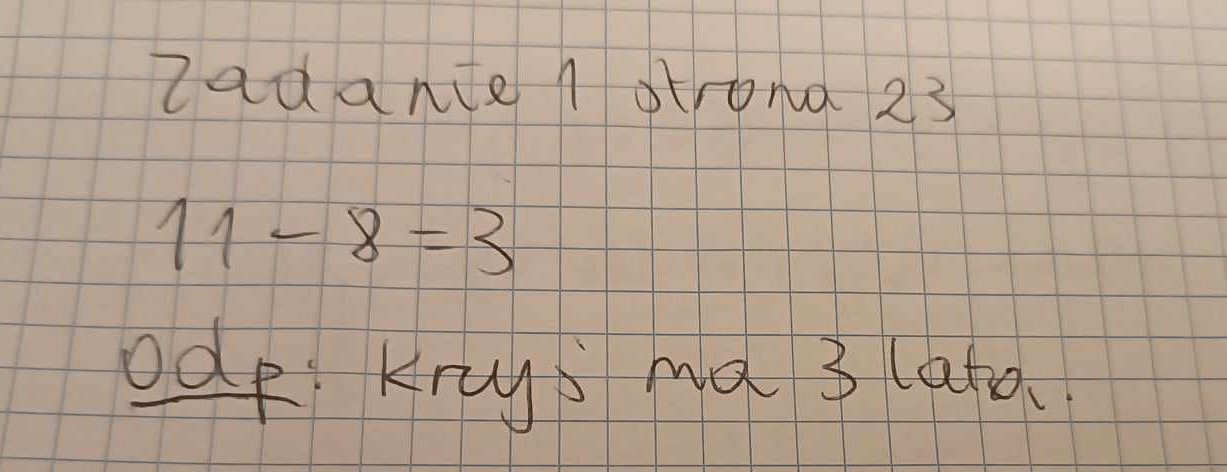
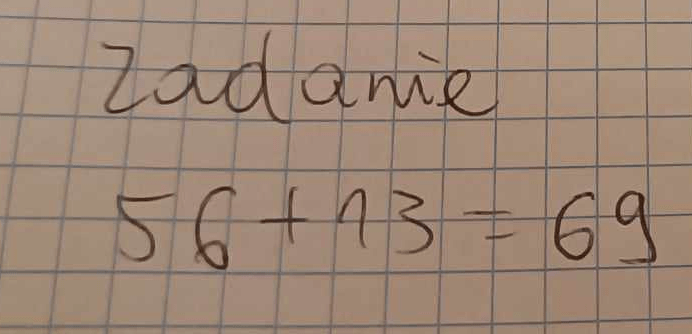
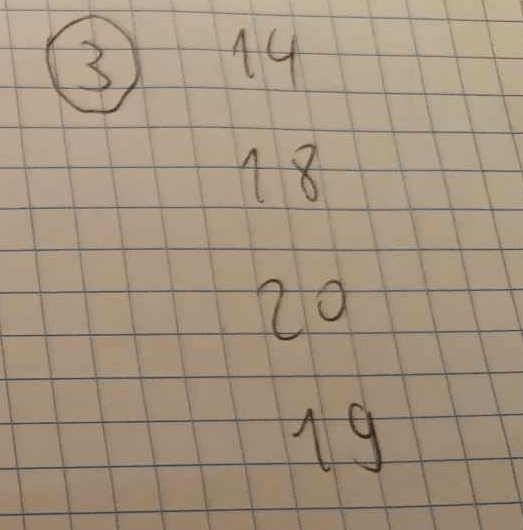
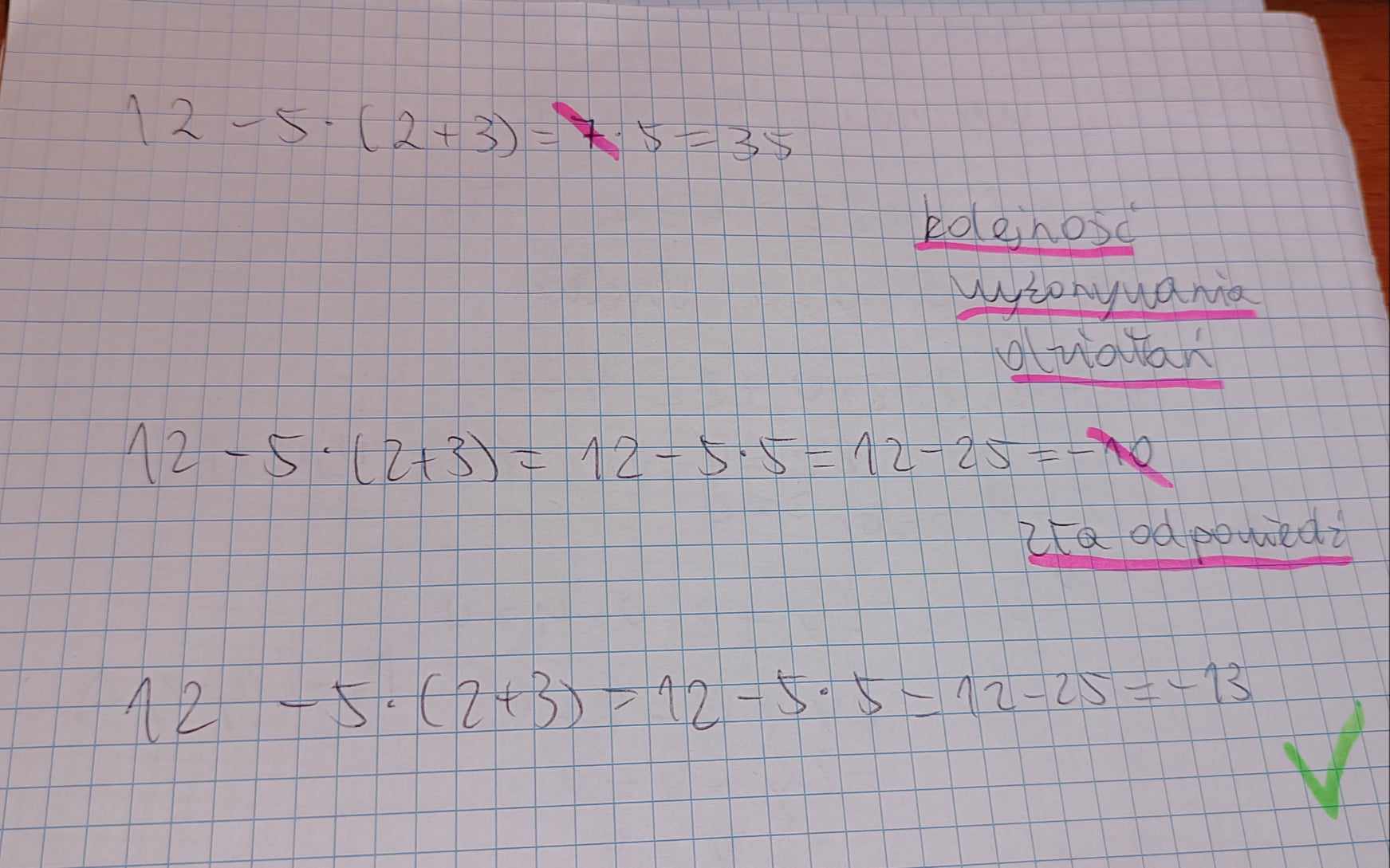



Świetny artykuł! Żałuję, że nie znałam tej strony kiedy pisałam maturę. Dużo by pomogło. Język, którym autor operuje jest lekki i przystępny, który dociera do kogoś kto swoją przygodę z matematyką zakończył kilka lat temu. Bardzo cenne wskazówki i szczerze zachęciły do powrotu do matematyki. Oby tak dalej, napewno zostanę na dłużej!
Świetnie ❤️ autor robi dobrą robotę.
Dziękuję bardzo!
Przepraszam za błędne kliknięcie ilości gwiazdek pod artykułem. Zrobiłam to przez przypadek, jeśli administrator może, to proszę o usunięcie moich głosów/głosu, a innych o nie sugerowanie się nimi.
Co do wpisu: dużo przydatnych informacji zawartych w jednym, konkretnym artykule. Zwięźle i na temat 👍
Powracając do tematu głosowania. Najprawdopodobniej zamiast 5 gwiazdek zaznaczyłam 3. Czyli średnia ocena jest wyższa; trochę matematyki i można to przeliczyć 👍 a jeśli ktoś ma ochotę na szybkie zadanie i sprawdzenie mnie: średnia ocen 5; po błędnym zagłosowania spadła do 4,3; łącznie oddano 3 głosy 😉
Jak się okazuje, nie zawsze dobrym pomysłem jest czytanie artykułów na telefonie, leżąc na łóżku, bo może się telefon wysmyknąć z rąk i narobić problemów. A telefon łapać trzeba, bez względu gdzie akurat się dotknie😅 mam pomysł dla autora na kolejny artykuł: sytuację w których telefony z klawiaturą są lepsze od tych z dotykiem. Kostek przemyśl i przepraszam za zamieszanie 😉